テクニカルサポートエンジニアリングチームの笠井 彰人です。
この記事は、Treasure Data CDPのWorkflowでベースになっているDigdagを使って遊んでみたという記事です。実際にTreasure Data CDPでWorkflowを扱う上ではほぼ役に立ちません。今回はタイトルにもある通り、モンテカルロ法を使って円周率を計算してみました。円周率を計算しよう思った理由は特に無いのですが、やったらできるかな?と思ったのでやってみました。
モンテカルロ法
モンテカルロ法は、Wikipediaには以下のように書いています。
モンテカルロ法(モンテカルロほう、(英: Monte Carlo method、MC)とはシミュレーションや数値計算を乱数を用いて行う手法の総称。
元々は、中性子が物質中を動き回る様子を探るためにスタニスワフ・ウラムが考案しジョン・フォン・ノイマンにより命名された手法。カジノで有名な国家モナコ公国の4つの地区(カルティ)の1つであるモンテカルロから名付けられた。ランダム法とも呼ばれる。
モンテカルロ法で円周率を求める場合、長さが1の正方形の上にランダムに点をうち、その座標を計算して円周率の近似を求めていきます。 つまり、以下のような、1×1の正方形について、半径1の円を描きます(単位円の1/4の面積をもちます)。
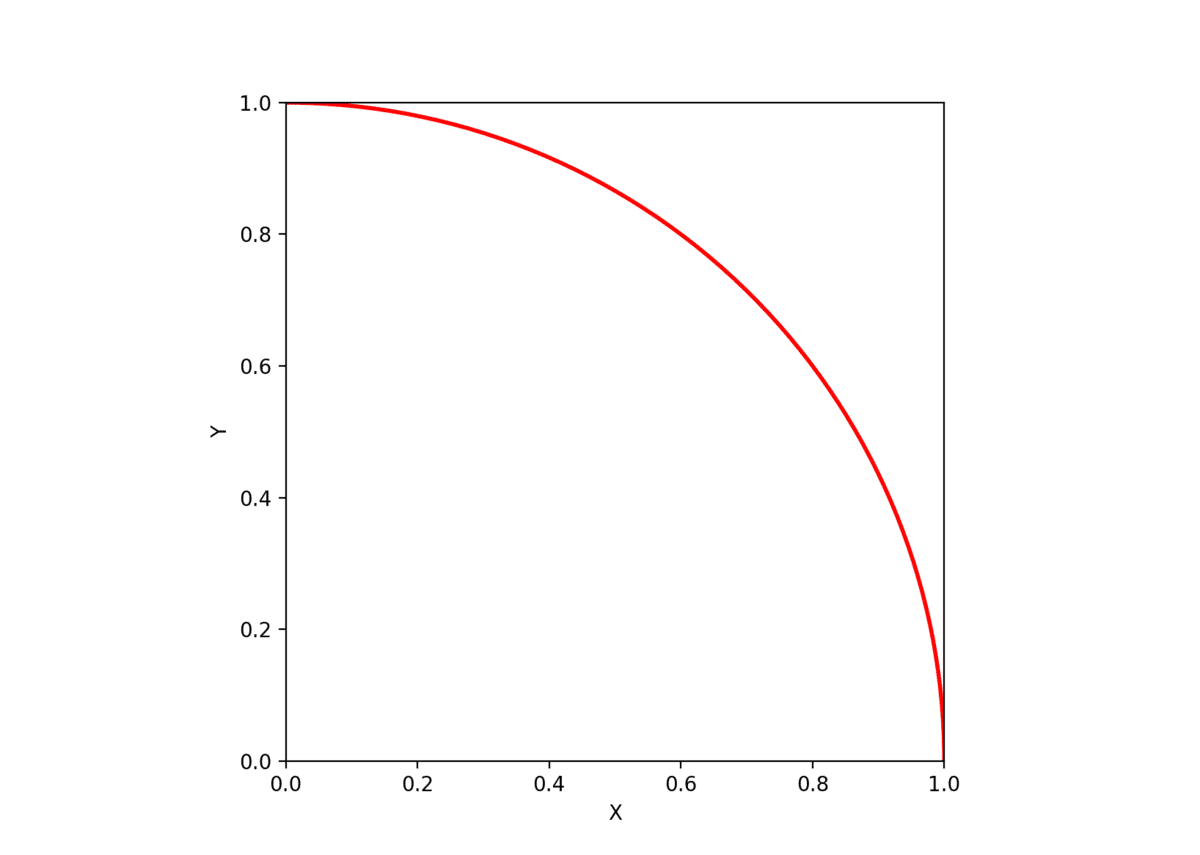
ここに、ランダムにいくつか点を打ち座標を見ていきますが、このとき 座標 (x,y) が弧の内部に存在するものだけをカウントします。 下の図は、 xy 平面上にランダムに点をプロットした図です。
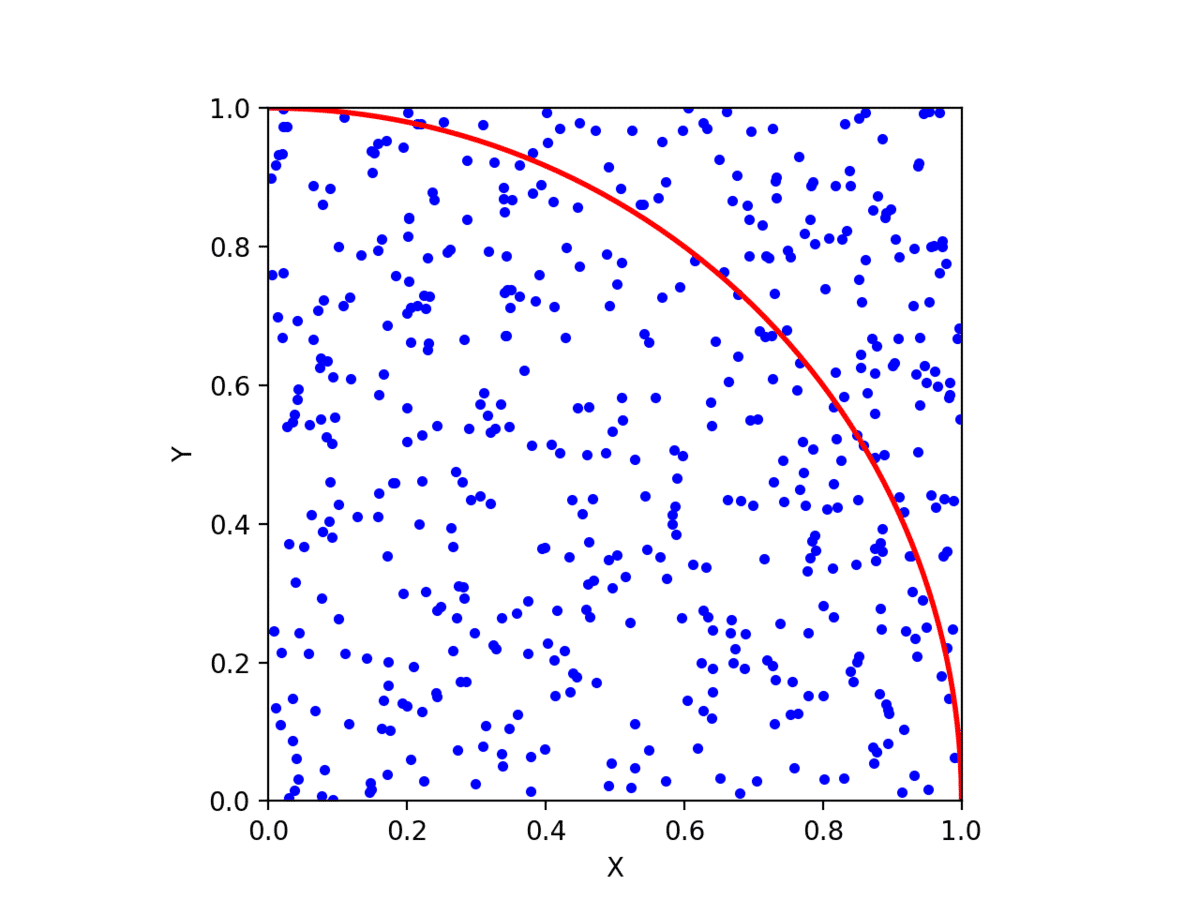
単位円の方程式は x2+y2=1 なので、平面上の座標 x と y の値をそれぞれ2乗した値の和が1未満であれば、円の内部の座標と判断できます。最後にカウントを点を打った回数で割った値に4を掛けておしまいです。 ここではかなり大雑把に書いているので、興味があれば検索してみると正しい理解が得られるはずです。ちなみに、C言語で書いてみるとだいたい以下のような感じになるかと思います。
#include#include #include #define LOOP 100000000 int main(void) { int count = 0; double x, y, pi; srand((unsigned int)time(NULL)); for (int i = 0; i < LOOP; ++i) { x = (double)rand() / RAND_MAX; y = (double)rand() / RAND_MAX; if ((x * x + y * y) < 1.0) { count++; } } pi = (double)count / LOOP * 4; printf("PI = %fn", pi); return 0; }
Digdag で円周率を求める
やっていることは既に書いた通り、
- 0.0 ~ 1.0 までの数値を2つ用意して、それぞれ変数 x, y に割り当てる。また、カウント用の変数も用意する。
- x, y それぞれの2乗の和が1未満であればカウントを増やし、 1 以上であれば何もしない
- 最後にカウント数とループした数の商に4を掛ける
dig ファイルとしては以下のような感じになりました。
_export:
num: 128
+setup:
param_set>:
key: 0
+calc:
loop>: ${num}
_do:
+repeat:
_export:
x: ${Math.random()}
y: ${Math.random()}
if>: ${(x * x + y * y) < 1.0}
_do:
+get_count:
param_get>:
key: count
+set_count:
param_set>:
key: ${parseInt(count) + 1}
+get_var:
param_get>:
key: value
+pi:
echo>: ${(value / num * 4).toPrecision(5)}
_prallel ができたらもうちょっと高速化できるかもしれないですが、countを数え上げるときにロックをとることができないので、シーケンシャルに処理しています。 変数の更新する必要があるので、param_set、 param_getを使いました。 このオペレータはPostgreSQLかRedisが必要であるため、Treasure Data CDPのWorkflowで試しても動きません。そのため、ローカルのPCから実行します。
モンテカルロ法による円周率の計算は、ランダムに打った点の数が多いほど(ループ回数が多いほど)、 3.141592.... の値に近づいていくので、精度も検証してみました。 今回はparam_set / param_getのためにRedisを使いました。 理想は1億ループくらい回してみたいですが、Digdagは実行可能なタスク上限が1000なので、ループ回数が多いと途中で上限に到達してエラーになってしまうため、最大200ループにしています。
| 試行回 | 25 loop | 50 loop | 100 loop | 150 loop | 200 loop |
| 1 | 3.2000 | 3.1200 | 3.3200 | 3.2267 | 3.1000 |
| 2 | 3.2000 | 3.1200 | 3.3200 | 3.2267 | 3.1000 |
| 3 | 3.2000 | 2.8800 | 3.0000 | 3.2800 | 3.0800 |
| 4 | 3.0400 | 3.2000 | 3.2800 | 3.2800 | 3.1600 |
| 5 | 3.3600 | 2.8800 | 2.9600 | 3.2000 | 3.1800 |
| 6 | 2.7200 | 3.1200 | 3.2400 | 3.3333 | 3.2000 |
| 7 | 3.0400 | 3.2800 | 3.1600 | 3.3067 | 3.1600 |
| 8 | 3.3600 | 3.5200 | 3.4000 | 3.0400 | 3.0800 |
| 9 | 3.2000 | 3.2000 | 3.2800 | 2.9867 | 3.4000 |
| 10 | 2.7200 | 3.2800 | 3.1200 | 3.1200 | 3.2400 |
| # of loops | 平均値 | πと平均値の差の絶対値 (π=3.141592) |
| 25 | 3.072000 | 0.069592 |
| 50 | 3.152000 | 0.010408 |
| 100 | 3.196000 | 0.054408 |
| 150 | 3.192010 | 0.050418 |
| 200 | 3.186000 | 0.044408 |
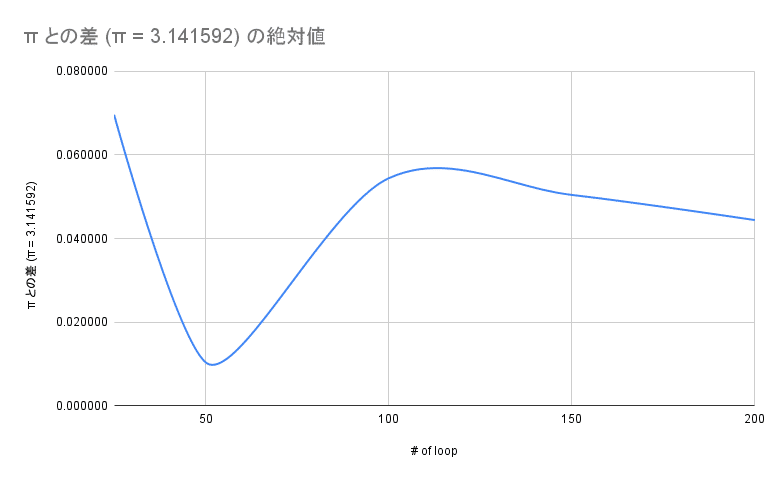
ループ回数は25回、50回、100回、150回、200回で、それぞれ10回ずつ実行し、 π との差を出しています。この差が小さいものほど精度が高いといえます。 結果としては、50回ループの検証が一番精度が高いという結果になってしまいましたが、高々200回のループの計算を10回しか試行していないので、まぁこんなものかなという感じですね。
おわりに
さてDigdagでもそれっぽい数値計算もできそうなことがわかりました。 今回は通常業務ではまず間違いなく使わない利用方法で、かつ本来は定常的に実行するタスクを人力に依らずに自動で実行するときに有用なツールなので、この記事のようなプログラムっぽい挙動の処理を書きたい場合は、YAMLベースのDigdagで頑張るよりはお好みのプログラミング言語を使ってプログラムを書いてしまったほうが速いし簡単です。Workflowであれば、Custom Scriptを使って処理を書いたほうが良いケースです。
ただ、今まで業務で触れてこなかったオペレータや変数の扱い方を考えることができるので、ひょっとしたら今後何かのWorkflowを作るときの引き出しが増えることがあるかもしれないので、もし何か思いついたときは遊んでみてもよいかもしれません。